Implied Interest Rate Volatility and XVA: How the One-Factor Hull-White Model is Weathering Changing Markets

by Christoph M. Puetter and Stefano Renzitti

Over the past year or so, interest rate volatilities have shifted considerably. Prior to 2022, leaving the more turbulent first half of 2020 aside, the financial markets in Europe and the U.S. were characterized by relatively low implied swaption volatility levels. But since the beginning of 2022, short-dated implied swaption volatilities have significantly increased and doubled or tripled in magnitude (as of mid-2023). Longer-dated implied swaption volatilities also noticeably increased, albeit more moderately. As a result, at-the-money implied swaption volatility surfaces are not only reaching fresh heights but are evolving their shapes and orientations, as well (Figure 1).

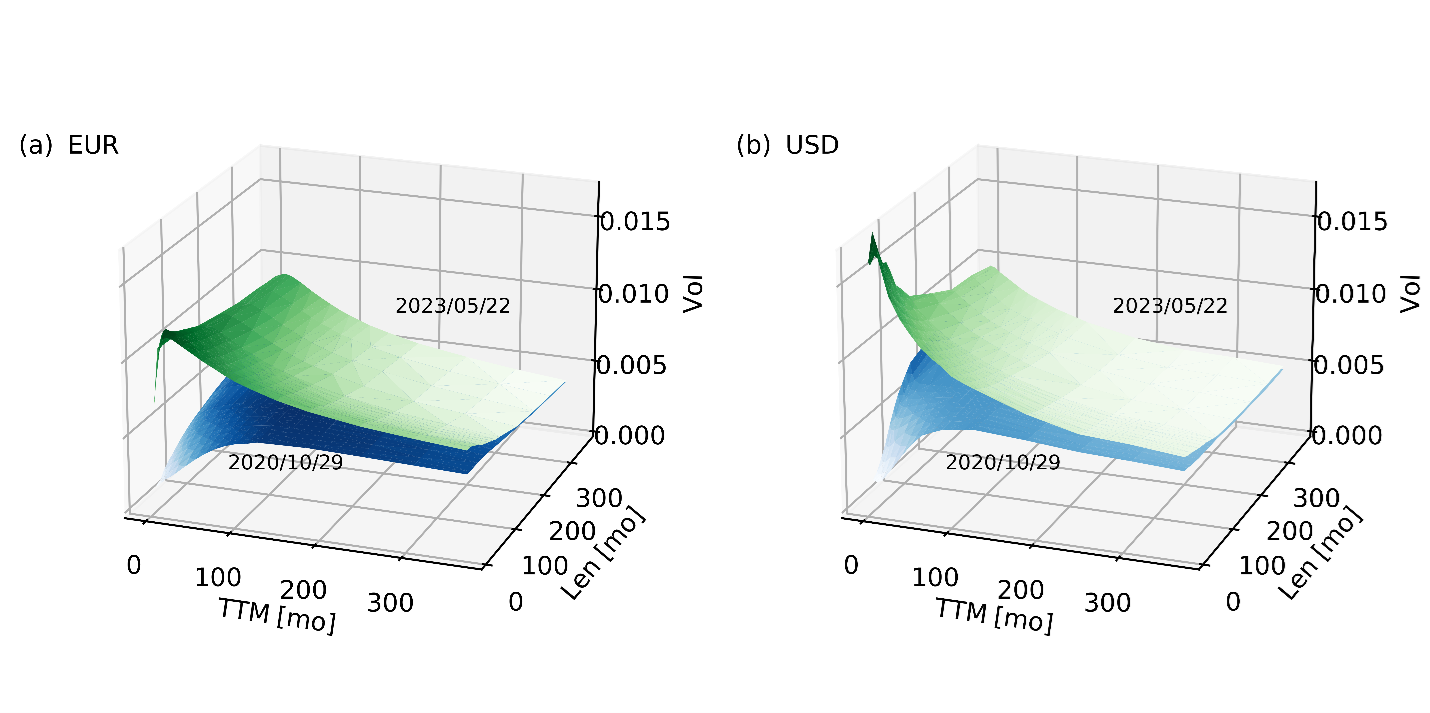
Figure 1. At-the-money (normal, annualized) implied swaption volatility surfaces for (a) EUR and (b) USD on 2020/10/29 (blue) and 2023/05/22 (green).

One-factor Hull-White interest rate model calibration

The one-factor Hull-White interest rate model is a popular all-purpose workhorse for the simulation and calculation of derivative valuation adjustments (XVAs) of interest rate portfolios. Its main model parameters are the (scalar) mean reversion parameter and the (time-dependent) short rate volatility. The latter is routinely calibrated to market-implied swaption volatilities, while the former is typically set according to some criterion or user preference. The mean reversion parameter ordinarily has a considerable impact on the overall silhouette of the model-implied swaption volatility surface, controlling, for instance, its slope along the tenor axis [1, 2]. The short rate volatility, on the other hand, approximately governs the term structure along the expiry axis and is often used to capture volatility characteristics relevant for the valuation of an interest rate portfolio or of risk metrics such as the credit valuation adjustment (CVA). To compute XVAs accurately and efficiently, we find monthly updates for the mean reversion parameter and daily updates for the short rate volatility to be reasonable. To update the mean reversion parameter, we minimize the overall (weighted) discrepancy between model- and market-implied volatilities across the at-the-money swaption volatility surface away from the instruments used for the short rate calibration. The latter are matched exactly as the result of the short rate calibration. Further details concerning the one-factor Hull-White model calibration for XVA are outlined in two papers by Puetter and Renzitti [3, 4].

Swaption volatilities, mean reversions, and risk-free rate yields

The short-dated corner of the at-the-money market-implied swaption volatility surface is often influenced by economic outlook and monetary policy expectations. As such it behaves similarly to the level and slope of the risk-free rate yield curve, which changes as the market prospects change. When a central bank lowers rates and/or economic activity is relatively predictable, the market-implied swaption volatilities in the short-dated corner tend to be low, forcing the volatility surface to assume a more horizontal orientation. As a result, the calibrated mean reversion parameter tends to be close to zero and can even turn negative. When the central bank increases rates and/or economic shocks appear, the opposite happens. The volatility surface tends to rise and slope more steeply away from short-dated expiries, leading to higher calibrated mean reversion values.

Panels (a) and (c) of Figure 2 also corroborate the correlated behavior of the implied swaption volatility surface and the risk-free rate yield curve. In fact, both the calibrated mean reversions for the euro (EUR) and the U.S. dollar (USD) and the 10-year yields of the euro short-term rate (ESTR) and the secured overnight financing rate (SOFR) curves appear to foreshadow the eventual rise of the central bank rates in Europe and the U.S. in mid and early 2022, respectively (see the steps in the overnight yields).

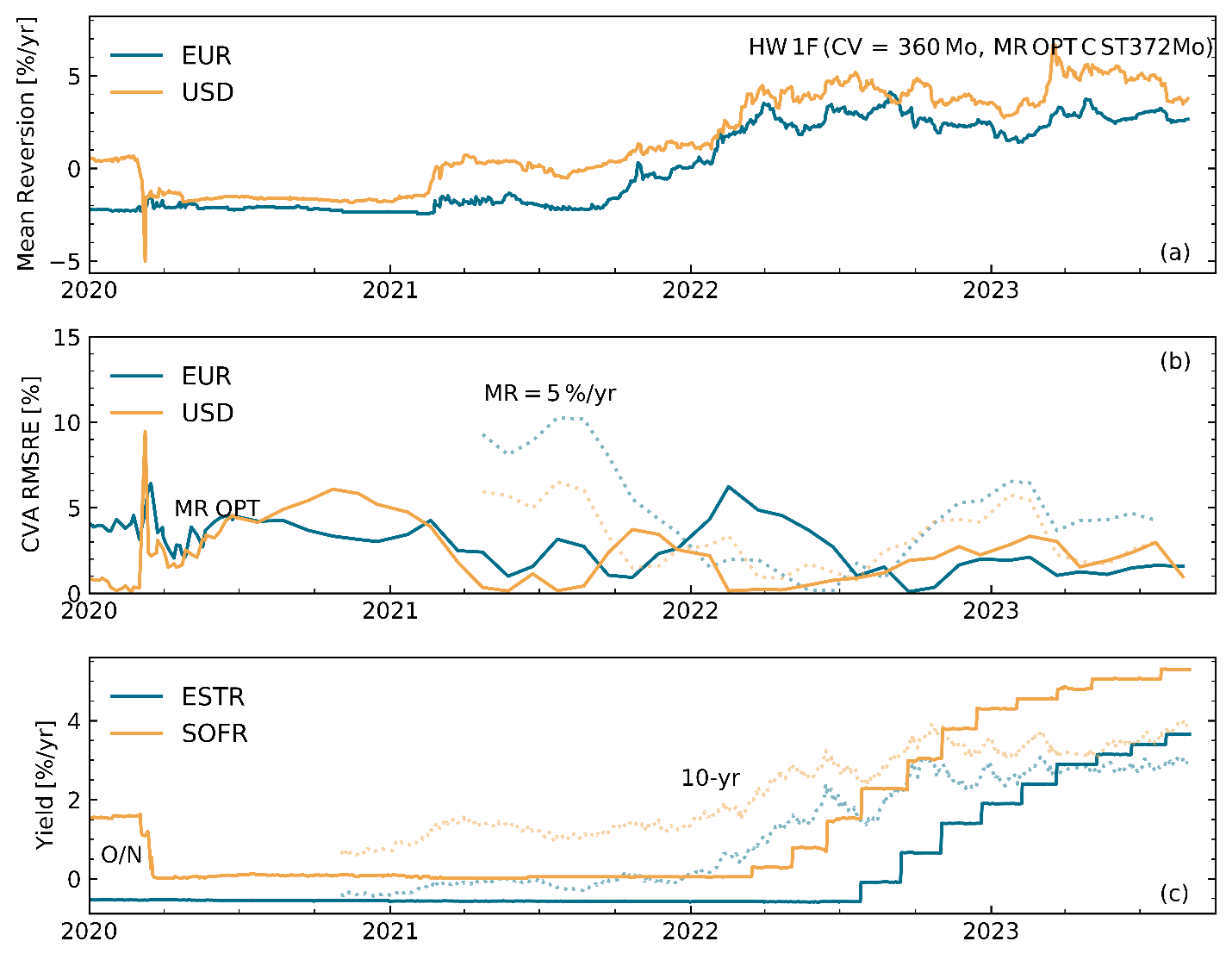
Figure 2. (a) Calibrated mean reversion time series for the one-factor Hull-White interest rate model (shown for daily calculation frequency); the short-rate calibration is based on a 30-year swaption chevron pattern [3]). (b) Corresponding relative CVA discrepancies (monthly frequency) for calibrated (MR OPT, solid lines) and constant mean reversion parameters (MR = 5 %/yr, dotted lines, time series starts on 2021/04/23). (c) Corresponding risk-free rate yields for overnight (O/N, solid curves) and intermediate (10-yr, dotted curves, time series start on 2020/11/01) tenors (daily frequency).

How have the CVA calculations fared recently?

The goal of the mean reversion calibration is to specify a more accurate and more broadly applicable interest rate simulation model for estimating XVAs. To benchmark the accuracy, we use a portfolio of at-the-money interest rate swaps with varying lengths of up to 30 years and compute the individual CVAs based on a fully calibrated (mean reversion and short rate) one-factor Hull-White model. We compare them with the corresponding exact market-implied CVAs (derived from swaption prices [3]) and measure the relative discrepancy via a root mean square relative error (RMSRE) metric. This error metric is displayed in panel (b) of Figure 2 and shows that the overall CVA discrepancy is still remarkably small (compared also with the results in [3]). The CVA RMSRE is consistently of the order of 5% or less. (The CVA RMSRE for EUR briefly breaches 5% in the first half of 2022, which is likely triggered by the robustness constraint imposed during the mean reversion optimization process [4].)
To contrast with the alternative of a partially calibrated one-factor Hull-White model, we fix the mean reversion parameter at 5%/year, calibrate the short rate volatility as before, and repeat the CVA calculations. The resulting CVA RMSRE is also shown in panel (b) of Figure 2 (dotted lines). Here, the CVA discrepancy appears to be larger, but is still respectable as the CVA RMSRE stays largely below 10%. During the first half of 2022, it even undershoots the CVA RMSRE for the mean reversion-optimized EUR equivalent. In either case, the CVA computations also benefit substantially from the instrument choice for the short rate volatility calibration. Presently, the short rate calibration is based on a chevron pattern of calibrating swaptions. When switching to a diagonal, co-terminal pattern, the CVA RMSREs tend to become much larger, assuming values of 10%-20% for the full calibration approach and greater for the partial calibration approach (not shown).

In summary, the mean reversion parameter of the one-factor Hull-White model is an important variable with global impact for the valuation of interest rate instruments. As illustrated here, it is advantageous to update this parameter occasionally to account for shifting market regimes such as bouts of rapid quantitative easing and quantitative tightening by central banks.

References
[1] Andersen L. B. G., & Piterbarg, V. V. (2010). Interest Rate Modeling, Volume 2: Term Structure Models. Atlantic Financial Press.
[2] Guerri, S., Nakabayashi, M., & Wong, T. (2010). Calibration Methods of Hull-White Model. SSRN Working Paper. Retrieved from http://dx.doi.org/10.2139/ssrn.1514192
[3] Puetter, C. M., & Renzitti, S. (2020). One-Factor Hull-White Model Calibration for CVA Part I: Instrument Selection with a Kink. Wilmott Magazine 2020 (110), 72-76.
[4] Puetter, C. M., & Renzitti, S. (2020). One-Factor Hull-White Model Calibration for CVA Part II: Optimizing the Mean Reversion Parameter. Wilmott Magazine 2020 (110), 77-81.

S&P Global provides industry-leading data, software and technology platforms and managed services to tackle some of the most difficult challenges in financial markets. We help our customers better understand complicated markets, reduce risk, operate more efficiently and comply with financial regulation.

This article was published by S&P Global Market Intelligence and not by S&P Global Ratings, which is a separately managed division of S&P Global.