Featured Topics
Featured Products
Events
S&P Global Offerings
Featured Topics
Featured Products
Events
S&P Global Offerings
Featured Topics
Featured Products
Events
S&P Global Offerings
Featured Topics
Featured Products
Events
Financial and Market intelligence
Fundamental & Alternative Datasets
Government & Defense
Professional Services
Banking & Capital Markets
Economy & Finance
Energy Transition & Sustainability
Technology & Innovation
Podcasts & Newsletters
Financial and Market intelligence
Fundamental & Alternative Datasets
Government & Defense
Professional Services
Banking & Capital Markets
Economy & Finance
Energy Transition & Sustainability
Technology & Innovation
Podcasts & Newsletters
ARTICLES & REPORTS — Sep 27, 2023
Christoph M. Puetter and Stefano Renzitti
The exchange of collateral is an important counterparty credit risk mitigant and a common practice in the over-the-counter derivative market that is typically prescribed or strongly encouraged by regulators either via margin rules[i] or through capital requirements[ii]. The nominal margin amount for a portfolio—the amount of cash denominated in the portfolio's currency to be posted or received as collateral—is based on the mark-to-market value in the case of variation margin and on value-at-risk in the case of initial margin. Depending on the details of the credit support annex, cash denominated in currencies other than the portfolio's currency, as well as an array of non-cash assets such as sovereign and corporate bonds of different maturities or equities, collectively known as physical collateral, is often also permitted as collateral.
Assuming the standard setup for counterparty credit risk where trade and margin flows cease at counterparty default, the counterparty credit exposure is subject to two sources of uncertainty at close-out: the value of the portfolio and the value of the collateral basket. Both can change materially and suddenly over the course of the close-out, particularly when hard (or systemic) wrong-way risk conditions apply. For example, it might be convenient and cheap to post Japanese corporate bonds as collateral to support a USD-denominated derivative portfolio, but if the counterparty is a large or systemically important institution for JPY and/or USD markets and defaults unexpectedly, portfolio and collateral values could jump and sharply diverge. The suddenness and sharpness distinguish this type of wrong-way risk from specific and general wrong-way risk, which are more gradual in expectation and impact.
Typically, the jump in the portfolio value dominates the hard wrong-way risk exposure. Jumps in the collateral asset values are of secondary importance but may matter under certain circumstances. The literature has focused mainly on the former. To complete the picture, we take a closer look at when and how collateral asset value jumps matter for hard wrong-way risk exposures.
To examine this issue, we apply a jump-at-default modeling approach. Jump-at-default modeling approaches are a simple and effective way to deal with hard wrong-way risk, and work by inferring default-conditioned counterparty credit exposures from unconditional baseline exposure simulations[iii][iv]. It is relatively easy to extend the standard jump-at-default approaches that usually ignore physical collateral to the case where trade parties can take advantage of the collateral optionality often embedded in credit support agreements.
Whether the impact of collateral value jumps is material or not depends largely on the moneyness of the portfolio. Consider, for example, a portfolio between a bank and a counterparty that is subject to a credit support agreement that focusses on the daily exchange of variation margin only and allows a range of collateral assets to be posted by either side with zero haircuts, zero thresholds, and zero minimum-transfer amounts. With this margining setup, the counterparty credit exposure at close-out is effectively determined as the difference between the increment in the portfolio value and the increment of collateral basket value over the close-out period (margin period of risk). In short, assuming a single-asset collateral basket, the exposure is:
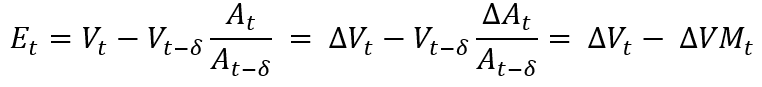
where δ denotes the close-out period, Vt and At are time-t portfolio and collateral asset values, respectively, ΔVt = Vt - Vt-δ and ΔA = At - At-δ the corresponding increments, and ΔVMt is the collateral basket value increment defined via the last equation. For a typical derivative portfolio, the portfolio value increment itself roughly scales with the portfolio's notional, whereas the collateral basket value increment is proportional to the nominal margin amount, which is equivalent to the portfolio's mark-to-market at the last successful margin call (the start of the close-out period). Depending on the portfolio's moneyness, the effective gearing of the collateral basket value increment can be smaller or larger and controls the impact of the collateral basket on the jump-at-default counterparty credit exposure.
To illustrate this point, first consider the extreme case that the portfolio is deep-in-the-money and collateralized with some non-cash asset. For simplicity, we model this case via a portfolio consisting of an in-the-money 10-year USD fixed-coupon bond (not a derivative but as effective for the present purpose) and a collateral basket composed of fresh 10-year T-Bonds that gets updated at each margin call date. Portfolio and collateral basket are sensitive to the same underlying risk factors initially but decouple over time as their maturities diverge. Table 1 shows that if only diffusive risk factor processes are simulated (no jumps), counterparty credit risk measures such as credit valuation adjustment (CVA), debit valuation adjustment (DVA), and the average potential future exposure (PFE95, taken at the 95th percentile and averaged over the lifetime of the portfolio), are relatively small as a fraction of the portfolio notional. Under systemic default, however, risk factors may jump. Assume that the main risk factors driving the 10-year T-bonds experience such jumps and induce a sudden decrease in the collateral basket value by 10% over the close-out period, while the portfolio remains unaffected (collateral jump only). This jump scenario is strongly skewed and leads to a significant increase in counterparty credit exposure that is reflected by the 30-fold increase in CVA and the 10-fold increase in PFE95. If, more consistently, the portfolio is also subjected to the same risk factor jumps, CVA and PFE95 risk measures then shrink to about a half (portfolio & collateral jumps). This behavior is intuitive and indicates that the collateral is quite effective in reducing counterparty credit risk, at least at the beginning when the maturities of the portfolio and collateral line up. But as the portfolio ages and matures, the portfolio in fact becomes less and less sensitive to the risk factor jumps, which results in a continually growing counterparty credit exposure that eventually is dominated by the collateral.
Table 1. Selected counterparty credit risk measures for a collateralized, deep-in-the-money, 10-year USD fixed-coupon bond and different jump-at-default dynamics. The collateral basket consists of either USD cash (for reference) or 10-year T-bonds. Close-out period amounts to 14 days. Valuation is in USD. All values are expressed in basis points of the portfolio notional.
|
CVA |
DVA |
CVA-DVA |
PFE95 |
|
|
No jumps (USD cash) |
2.0 |
2.0 |
0.0 |
127.9 |
|
No jumps (T-bonds) |
2.4 |
2.4 |
0.0 |
111.8 |
|
Collateral jumps only (T-bonds) |
72.0 |
0.0 |
72.0 |
1078.6 |
|
Portfolio and collateral jumps (T-bonds) |
40.4 |
0.0 |
40.4 |
548.3 |
For reference, risk measures for USD cash collateral only are also displayed in Table 1 and the following tables. For no-jump, diffusion-only close-out dynamics, the collateral choice appears to affect CVA, DVA, and PFE95 only in a limited manner. Collateralization with USD cash collateral, therefore, is relatively representative in this circumstance.
Next, we contrast with the opposite case, where the jump-at-default impact of the collateral basket on counterparty credit exposure is insignificant as the portfolio value stays at-the-money by design, which in turn keeps the nominal variation margin amount near zero. Here we take the portfolio to consist of a resetting mark-to-market JPY/USD basis swap and simply collateralize with JPY cash. We suppose that exposures and risk measures are all valued in USD. Table 2 shows that, again, under diffusion-only risk factor dynamics, CVA, DVA, and PFE95 are relatively small. Quanto credit default swap spreads suggest, however, that the JPY/USD exchange rate may depreciate by up to 30% under systemic default conditions[v]. Including a JPY/USD exchange rate jump of that size in the collateral close-out dynamics has no impact on the counterparty credit exposure (remember that the collateral collected is close to zero due to the resetting feature and 30% of close to zero is still close to zero), but including the exchange rate jump in the portfolio close-out dynamics results in an enormous wrong-way risk exposure (the portfolio value change is proportional to 30% · Notional · FXt / FX0). Consequently, CVA increases by a factor of more than 40 and PFE95 by a factor of more than 15 compared to the no-jump JPY cash collateral scenario.
Table 2. Selected counterparty credit risk measures for a collateralized, resetting mark-to-market 10-year JPY/USD basis swap (pay JPY, receive USD) and different jump-at-default dynamics. The collateral basket consists of either USD cash (for reference) or JPY cash. Close-out period amounts to 14 days. Valuation is in USD. All values are expressed in basis points of portfolio notional.
|
CVA |
DVA |
CVA-DVA |
PFE95 |
|
|
No jumps (USD cash) |
6.0 |
6.0 |
0.0 |
313.6 |
|
No jumps (JPY cash) |
6.0 |
6.0 |
0.0 |
313.4 |
|
Collateral jumps only (JPY cash) |
6.9 |
7.1 |
-0.2 |
363.5 |
|
Collateral and portfolio jumps (JPY cash) |
260.9 |
0.0 |
260.9 |
4719.4 |
More common cases, where a portfolio can move away-from-the money, making collateral jump-at-default dynamics somewhat relevant, typically fall between these two extremes. To demonstrate, Table 3 shows the risk measures for a collateralized non-resetting JPY/USD basis swap that, except for the reset feature, is almost identical to the collateralized resetting mark-to-market JPY/USD basis swap just discussed. Under no-jump, diffusion-only dynamics, both types of collateralized cross-currency basis swaps exhibit similar levels of CVA, DVA, and PFE95, which is expected as short-term diffusion of the portfolio governs the exposures. Including the JPY/USD exchange rate jump in the collateral close-out dynamics (collateral jumps only) gives rise to a modest CVA increase, but substantial DVA and PFE95 hikes. This is the result of the JPY/USD devaluation reducing the (absolute) value of the collateral basket over the close-out period independent of moneyness, leading to increased expected negative and expected positive exposures, and the observation that in the present instance, the non-resetting JPY/USD basis swap tends to move out-of-the-money over its lifetime. Including the exchange rate jump also in the portfolio close-out dynamics leads to significantly enhanced CVA and PFE95 amounts and nearly vanishing DVA. In contrast to the resetting mark-market JPY/USD basis swap above, the jump increment in the collateral basket value is non-negligible and positively or negatively correlated with the portfolio value increment, depending on moneyness. CVA and PFE95 turn out to be large but not as extreme as in the previous case.
Table 3. Selected counterparty credit risk measures for a collateralized, non-resetting 10-year JPY/USD basis swap (pay JPY, receive USD) and different jump-at-default dynamics. The collateral basket consists of either USD cash (for reference) or JPY cash. Close-out period amounts to 14 days. Valuation is in USD. All values are expressed in basis points of portfolio notional.
|
CVA |
DVA |
CVA-DVA |
PFE95 |
|
|
No jumps (USD cash) |
6.0 |
6.0 |
0.0 |
313.8 |
|
No jumps (JPY cash) |
5.1 |
4.9 |
0.2 |
268.5 |
|
Collateral jumps only (JPY cash) |
6.2 |
50.1 |
-43.9 |
504.9 |
|
Collateral and portfolio jumps (JPY cash) |
218.0 |
0.2 |
217.7 |
3454.8 |
Finally, we consider the consequences for a collateralized 10-year USD interest rate swap (Table 4). The bank pays fixed coupons and receives float coupons. In contrast to the portfolios above, a notional exchange at maturity is absent. The collateral basket again consists of fresh 10-year T-bonds that may jump down in value during close-out. Even though the interest rate swap can be relatively far away-from-the-money, the portfolio value increments tend to dominate over the collateral basket value increments. Given the cashflow directions of the interest rate swap, portfolio value increments and the collateral basket value increments are negatively (positively) correlated for in-the-money (out-of-the-money) trajectories. Therefore, including jumps in both portfolio and collateral close-out dynamics results in hard wrong-way risk behavior and substantially elevated CVA and PFE95 levels. The increase in CVA and PFE95 is further enhanced by wrong-way risk behavior of the collateral term when in-the-money and attenuated when out-of-the-money. We note that here the jump impact on the portfolio is relatively constant with time, unlike the case of the fixed coupon bond.
Table 4. Selected counterparty credit risk measures for a collateralized 10-year USD interest rate swap (pay fixed, receive float) with varying moneyness and different jump-at-default dynamics. The swap is taken to be far in-the-money (ITM, par - 300 bp), at-the-money (ATM, par), and far out-of-the-money (OTM, par + 300 bp). The collateral basket consists of either USD cash (for reference) or T-bonds. Valuation is in USD. Close-out period amounts to 14 days. All values are expressed in basis points of portfolio notional.
|
CVA |
DVA |
CVA-DVA |
PFE95 |
|
|
Far ITM |
||||
|
No jumps (USD cash) |
1.8 |
1.8 |
0.0 |
114.4 |
|
No jumps (T-bonds) |
2.4 |
2.4 |
0.0 |
153.0 |
|
Collateral jumps only (T-bonds) |
10.0 |
0.5 |
9.5 |
335.0 |
|
Portfolio and collateral jumps (T-bonds) |
39.0 |
0.0 |
39.0 |
713.8 |
|
ATM |
||||
|
No jumps (USD cash) |
2.0 |
2.0 |
0.0 |
129.0 |
|
No jumps (T-bonds) |
2.0 |
2.0 |
0.0 |
129.2 |
|
Collateral jumps only (T-bonds) |
3.0 |
3.3 |
-0.3 |
184.6 |
|
Portfolio and collateral jumps (T-bonds) |
32.3 |
0.0 |
32.3 |
602.3 |
|
Far OTM |
||||
|
No jumps (USD cash) |
2.2 |
2.2 |
0.0 |
143.5 |
|
No jumps (T-bonds) |
1.6 |
1.6 |
0.0 |
105.3 |
|
Collateral jumps only (T-bonds) |
0.4 |
10.4 |
-10.0 |
37.5 |
|
Portfolio and collateral jumps (T-bonds) |
25.6 |
0.0 |
25.6 |
491.1 |
The examples in this paper show that jump-at-default modeling of portfolio and collateral can manifest itself in a variety of counterparty credit risk behaviors. More details and examples, including different types of jump configurations, are discussed in an upcoming article[vi].
Learn more about the XVA solution from S&P Global Market intelligence.
[i] Basel Committee on Banking Supervision and Board of the International Organization of Securities Commissions (2020). Margin requirements for non-centrally cleared derivatives.https://www.bis.org/bcbs/publ/d499.pdf
[ii] Basel Committee on Banking Supervision (2010). Basel III: A global regulatory framework for more resilient banks and banking systems. Retrieved from https://www.bis.org/publ/bcbs189.pdf
[iii] Li, M., & Mercurio, F. (2015). Jumping with default: wrong-way risk modelling for CVA. Risk, November, 58-63.
[iv] Pykhtin, M., & Sokol, A. (2013). Exposure under systemic impact. Risk, September, 88-93.
[v] Chung, T.-K., & Gregory, J. (2019). CVA wrong-way risk: calibration using a quanto CDS basis. Risk, July, 1-6.
[vi] Puetter, C. M. & Renzitti, S. (2023). Forthcoming.
S&P Global provides industry-leading data, software and technology platforms and managed services to tackle some of the most difficult challenges in financial markets. We help our customers better understand complicated markets, reduce risk, operate more efficiently and comply with financial regulation.
This article was published by S&P Global Market Intelligence and not by S&P Global Ratings, which is a separately managed division of S&P Global.
Location
